Metacognitive Facilitation Research Paper

Research Papers

Metacognitive Facilitation

	White, B., & Frederiksen, J. "Metacognitive facilitation: An approach to making scientific inquiry accessible to all." In J. Minstrell and E. van Zee (Eds.), Inquiring into Inquiry Learning and Teaching in Science. (pp. 331-370). Washington, DC: American Association for the Advancement of Science, 2000.
	Metacognitive Facilitation: An Approach to Making Scientific Inquiry Accessible to All Barbara Y. White, University of California at Berkeley John R. Frederiksen, Educational Testing Service.
Contents	TABLE OF CONTENTS Abstract Introduction Facilitating Inquiry within the Classroom Research Community Facilitating Reflective Assessment within the Classroom Research Community Instructional Trials of the ThinkerTools Inquiry Curriculum An Overview of the Results The Development of Inquiry Expertise The Development of Physics Expertise The Impact of Understanding the Reflective Assessment Criteria The Implications of Our Findings Metacognitive Facilitation for Teachers Acknowledgments References Appendix A An Outline and Checklist for Your Research Reports Example Research Report Example Self Assessment
Abstract	ABSTRACT In the ThinkerTools Inquiry Project, researchers and teachers collaborated to create a computer-enhanced, middle-school, science curriculum that enables students to learn about the processes of scientific inquiry and modeling as they construct a theory of force and motion. The class functions as a research community. Students propose competing theories. They then test their theories by working in groups to design and carry out experiments using both computer models and real-world materials. Finally, they come together to compare their findings and to try to reach a consensus about the physical laws and causal models that best account for their results. This process is repeated as the students tackle new research questions that foster the evolution of their theories of force and motion. The ThinkerTools Inquiry Curriculum focuses on facilitating the development of metacognitive knowledge and skills as students learn the inquiry processes needed to create and revise their theories. Instructional trials in urban classrooms revealed that this approach is highly effective in enabling all students to improve their performance on various inquiry and physics measures. The approach incorporates a reflective process in which students evaluate their own and each other's research using a set of criteria that characterize good inquiry, such as reasoning carefully and collaborating well. When this reflective process is included, the curriculum is particularly effective in reducing the performance gap between low and high achieving students. These findings have strong implications for what such inquiry-oriented, metacognitively-focused curricula can accomplish, particularly in urban school settings in which there are many disadvantaged students. Furthermore, the process of metacognitive facilitation can also be helpful to teachers as they learn how to engage in and reflect on inquiry teaching practices.
Introduction	INTRODUCTION Science can be viewed as a process of creating laws, models, and theories that enable one to predict, explain, and control the behavior of the world. Our objective in the ThinkerTools Inquiry Project has been to create an instructional approach that makes this view of understanding and doing science accessible to a wide range of students, including lower-achieving and younger students. Our hypothesis is that this objective can be achieved by facilitating the development of the relevant metacognitive knowledge and skills: students need to learn about the nature and utility of scientific models as well as the processes by which they are created, tested, and revised. (See Brown [1984], Brown, Collins, and Duguid [1989], Bruer [1993], Collins and Ferguson [1993], Nickerson, Perkins, and Smith [1985], and Resnick [1987] for further discussions regarding the central role that metacognition plays in learning.) To test our hypothesis about making scientific inquiry accessible to all students by focusing on the development of metacognitive expertise, we created the ThinkerTools Inquiry Curriculum in which students construct and revise theories of force and motion. The curricular activities and materials are aimed at developing the knowledge and skills that students need to support this inquiry process. The curriculum begins by introducing students to a metacognitive model of research, called "The Inquiry Cycle," and a metacognitive process, called "Reflective Assessment," in which they reflect on their inquiry (see Figures 1 and 2). The Inquiry Cycle consists of five steps and provides a goal structure which students use to guide their inquiry. The curricular activities focus on enabling students to develop the expertise needed to carry out and understand the purpose of the steps in the Inquiry Cycle, as well as to monitor and reflect on their progress as they conduct their research. This is achieved via a constructivist approach that could be characterized as learning metacognitive knowledge and skills through a process of scaffolded inquiry, reflection, and generalization. We call this approach "metacognitive facilitation." 1. Scaffolded Inquiry. We designed scaffolded activities and environments to enable students to learn about inquiry as they engage in authentic scientific research. The scaffolded activities are aimed at helping them learn about the characteristics of scientific laws and models, the processes of experimental design and data analysis, and the nature of scientific argument and proof. The scaffolded environments, which include computer simulations (that allow students to create and interact with models of force and motion) and analytic tools (for analyzing the results of their computer and real-world experiments), make the inquiry process as easy and productive as possible at each stage in learning. These activities and environments enable students to carry out a sequence of activities that correspond to the steps in the Inquiry Cycle. Initially, the meaning and purpose of the steps in the Inquiry Cycle may be only partially understood by students. 2. Reflective Assessment. In conjunction with the scaffolded inquiry, students are introduced to a reflective process in which they evaluate their own and each other's research. This process employs a carefully chosen set of criteria that characterize expert scientific inquiry (such as "Being Systematic" and "Reasoning Carefully" as shown in Figure 2) to enable students to see the intellectual purpose and properties of the inquiry steps and their sequencing. By reflecting on the attributes of each activity and its function in constructing scientific theories, students grow to understand the nature of inquiry and the habits of thought that are involved. 3. Generalized Inquiry and Reflection. The Inquiry Cycle is repeated as the class addresses new research questions. Each time the cycle is repeated, some of the scaffolding is removed so that eventually the students are conducting independent inquiry on questions of their own choosing (as in the scaffolding and fading approach of Palincsar and Brown, 1984). These repetitions of the Inquiry Cycle in conjunction with reflection help students to refine their inquiry processes. Carrying out these processes in new research contexts also enables students to learn how to generalize the inquiry and reflection processes so that they can apply them to learning about new topics in the future.

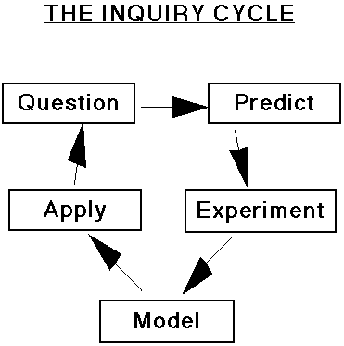
	Figure 1. A model of the scientific inquiry process which students use to guide their research.

	Figure 2. The criteria for judging research which students use in the Reflective Assessment Process.
Inquiry	FACILITATING INQUIRY WITHIN THE CLASSROOM RESEARCH COMMUNITY The project has established Classroom Research Communities in 7th, 8th, and 9th grade science classrooms in middle schools in Berkeley and Oakland. In these classes, inquiry is the basis for developing an understanding of the physics. Physical theories are not directly taught, but are constructed by students themselves. The idea is to teach students how to carry out scientific inquiry, and then have the students discover the basic physical principles for themselves by doing experiments and creating theories. The process of inquiry follows the Inquiry Cycle, shown in Figure 1, which is presented to students as a basis for organizing their explorations into the physics of force and motion. Inquiry begins with finding research questions, that is, finding situations or phenomena students do not yet understand which become new areas for investigation. Students then use their intuitions (which are often incorrect) to make conjectures about what might happen in such situations. These predictions provide them with a focus as they design experiments that allow them to observe phenomena and test their conjectures. Students then use their findings as a basis for constructing formal laws and models. By applying their models to new situations, students test the range of applicability of their models and, in so doing, identify new research questions for further inquiry. The social organization of the research community is similar to that of an actual scientific community. Inquiry begins with a whole-class forum to develop shared research themes and areas for joint exploration. Research is then carried out in collaborative research groups. The groups then reassemble to conduct a research symposium in which they present their predictions, experiments, and results, as well as the laws and causal models they propose to explain their findings. While the results and models proposed by individual groups may vary in their accuracy, in the research symposium a process of consensus building increases the reliability of the research findings. The goal is, through debate based upon evidence, to arrive at a common, agreed-upon theory of force and motion. Organization of the curriculum. The curriculum is based on a series of investigations of physical phenomena that increase in complexity. On the first day, students toss a hacky sack around the room while the teacher has them observe and list all of the factors that may be involved in determining its motion (how it is thrown, gravity, air resistance, etc.). As an inquiry strategy, the teacher suggests the need to simplify the situation, and this discussion leads to the idea of looking at simpler cases, such as that of one-dimensional motion where there is no friction or gravity (an example is a ball moving through outer space). The curriculum is, accordingly, organized around starting with this simple case (Module 1), and then adding successively more complicating factors such as introducing friction (Module 2), varying the mass of the ball (Module 3), exploring two-dimensional motion (Module 4), investigating the effects of gravity (Module 5), and analyzing trajectories (Module 6). At the end of the curriculum, students are presented with a variety of possible research topics to pursue (such as orbital motion, collisions, etc.), and they carry out research on topics of their own choosing (Module 7). For each new topic in the curriculum, students follow the Inquiry Cycle: 1. Question. As described above, the inquiry process begins with developing a research question such as, "What happens to the motion of an object that has been pushed or shoved when there is no friction or gravity acting on it?" 2. Predict. Next, to set the stage for their investigations, students try to generate alternative predictions and theories about what might happen in some specific situations that are related to the research question. In other words, they engage in "thought experiments." For example, in Module 1, they are asked to predict what would happen in the following situation. "Imagine a ball that is stopped on a frictionless surface, one that is even smoother than ice. Suppose that you hit the ball with a mallet. Then, imagine you hit the ball again in the same direction with the same size hit. Would the second hit change the velocity of the ball? If so, describe how it would change and explain why." In response to this question, some students might say, "the second hit does not affect the speed of the ball because it's the same size hit as the first;" while others might say, "it makes the ball go twice as fast because it gives the ball twice as much force;" and others might say, " it only makes the ball go a little bit faster because the ball is already moving." 3. Experiment. After presenting their predictions to the class, students break into research groups to design and carry out experiments to test their alternative theories. These investigations make use of both computer simulations and real-world experimental materials. a. Computer activities and experiments. Computer models and experiments are done using the ThinkerTools software that we developed for the Macintosh computer. This software enables students to interact with Newtonian models of force and motion (see Figure 3 which shows an example of a computer activity that students use in studying one-dimensional motion). It also lets students create their own models and experiments. Using simple drawing tools, students can construct and run computer simulations. Objects (such as the large circle shown in Figure 3) and barriers can be placed on the screen. (The objects are introduced to students as generic objects, simply called "dots," which are the pictorial equivalent of variables that students can map onto different objects such as space ships or billiard balls.) Students can define and change the properties of any object, such as its mass, elasticity (e.g., bouncy or fragile), and velocity. They can then apply impulses to the object to change its velocity using the keyboard or a joystick as in a video game. (Impulses are forces that act for a specified -- usually short-- amount of time like a kick or a hit.) Students can thus create and experiment with a "dot-impulse model" and can discover, for example, that when one applies an impulse in the same direction that the dot is moving, it increases the dot's velocity by one unit of speed. In this way, they can use simulations to discover the laws of physics and their implications.

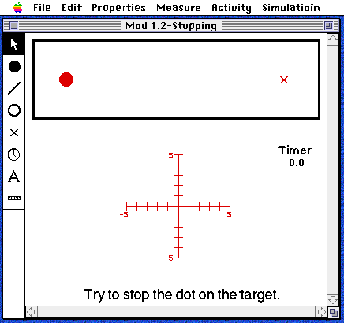
	Figure 3. The ThinkerTools Software: A modeling and inquiry tool for creating and experimenting with models of force and motion.
	Such software enables students to create experimental situations that are difficult or impossible to create in the real world. For example, they can turn friction and gravity on and off and can select different friction laws (i.e., sliding friction or gas/fluid friction). They can also vary the amount of friction or gravity to see what happens. Such experimental manipulations in which students dramatically alter the parameters of the simulation allow students to use inquiry strategies, such as "look at extreme cases," which are hard to utilize in real-world inquiry. This type of inquiry enables students to see more readily the behavioral implications of the laws of physics and to discover the underlying principles. A major advantage of the software is that it includes measurement tools which allow students to easily make accurate measurements of distances, times, and velocities that are difficult to make in real-world experiments. It also includes graphical representations of variables. For example, in Figure 3 there is a "datacross" which shows the x and y velocity components when the dot is moving. Also, as the dot moves, it can leave behind "dot prints" which show how far it moved in each second and "thrust prints" which show when an impulse was applied. In addition, the software provides analytic tools such as being able to step through time in order to analyze what is happening. These representations and analytic tools help students determine the underlying laws of motion. They can also be incorporated within the students' conceptual model to represent and reason about what might happen in successive time steps. Ideally, the software helps students construct conceptual models that are similar to the computers in that both use diagrammatic representations and employ causal reasoning in which they step through time to analyze events. In this way, such dynamic interactive simulations combined with these analytic tools can provide a transition from students' intuitive ways of reasoning about the world to the more abstract formal methods that scientists use for representing and reasoning about a system's behavior (White, 1993b). b. Real-world experiments. Students are also given a set of materials for conducting real-world experiments. These include "bonkers" (a bonker is a rubber mallet mounted on a stand), balls of varying masses, and measurement tools such as meter sticks and stop watches (see Figure 4). These tools are coordinated with those used in the ThinkerTools software. For instance, the bonker is similar to the joystick and is used to give a ball a standard-sized impulse. Using such materials, students design and carry out real-world experiments that are related to those done with the computer simulation. Students are also shown stop-motion videos of some of their experiments. Using frame-by-frame presentations, they can attach blank transparencies to the video screen and draw the position of a moving ball after fixed time intervals. These "dotprint analyses" allow them to measure the moment-by-moment changes in the ball's velocity.
	The Double-Bonk Experiment

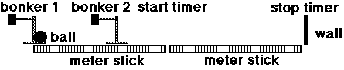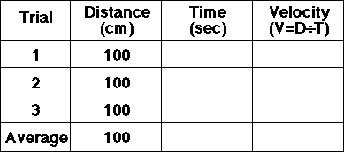
	Data Table

	Figure 4. An illustration of the double-bonk experiment along with the table that students use to record their data.
	4. Model. After the students have completed their experiments, they analyze their data to see if there are any patterns. They then try to summarize and explain their findings by formulating a law and a causal model to characterize their conclusions. Students' models typically take the form: "If A then B because ..." For example, "if there are no forces like friction acting on an object, then it will go forever at the same speed, because there is nothing to slow it down." The computer simulations combined with real-world experiments and the process of creating a model can help students to understand the nature of scientific models. To elaborate, the computer is not the real world; it can only simulate real-world behavior by stepping through time and using rules to determine how forces that are acting (like friction or gravity) will change the dot's velocity on that time step. Thus, the computer is actually using a conceptual model to predict behavior, just as the students will use the conceptual model they construct to predict behavior. In working with the computer, the students' task is to design experiments that will help them induce the laws that are used by the simulation. This is more straightforward than the corresponding real-world inquiry task. After all, objects in the real world are not driven by laws; rather, the laws simply characterize their behavior. One example of a modeling activity, which is carried out early in the curriculum, has students explain how their computer and real-world experiments could lead to different conclusions. They might say, for instance, that "the computer simulation does not have friction which is affecting our real-world experiments." Alternatively, they might say that "the real world does not behave perfectly and does not follow rules." Working with a computer simulation can thus potentially help students to develop metaconceptual knowledge about what scientific models are, and how laws can be used to predict and control behavior. It can also enable them to appreciate the utility of creating computer simulations that embody scientific laws and idealized abstractions of real-world behavior, and then of using such simulations to do experiments in order to see the implications of a particular theory. Based on the findings of their computer and real-world experiments, students prepare posters, make oral presentations to the class, and submit project reports. The Inquiry Cycle is used in organizing their reports and presentations. Students use writing, graphing, and drawing software (such as ClarisWorks) for analyzing their data and preparing their reports. Then, in a whole-class research symposium, they evaluate together the results of all the research groups, and choose the "best" laws and models to explain their findings. 5. Apply. Once the class chooses the best laws and causal models, students try to apply them to different real-world situations. For instance, they might try to predict what happens when you hit a hockey puck on ice. As part of this process, they investigate the utility of their laws and models for predicting and explaining what would happen. They also investigate the limits of their models (such as, "What happens if the ice isn't perfectly smooth?"), which inevitably raises new research questions (such as, "What are the effects of friction?"). This brings the class back to the beginning of the Inquiry Cycle and to investigating the next research question in the curriculum. The Inquiry Cycle is repeated with each of the seven modules of the curriculum. The physics the students are dealing with increases in complexity as the curriculum progresses and so does the inquiry. In the early stages of the curriculum, the inquiry process is heavily scaffolded. For example, in Module 1, students are given experiments to do and are presented with alternative possible laws to evaluate. In this way, they see examples of experiments and laws before they have to create their own. In Module 2, students are given experiments to do but have to construct the laws for themselves. Then, in Module 3, they design their own experiments and construct their own laws to characterize their findings (see Appendix A). By the end of the curriculum, the students are carrying out independent inquiry on a topic of their own choosing.
Reflective Assessment	FACILITATING REFLECTIVE ASSESSMENT WITHIN THE CLASSROOM RESEARCH COMMUNITY In addition to the Inquiry Cycle which guides the students' research and helps them to understand what the research process is all about, we also developed a set of criteria for characterizing good scientific research. These are presented in Figure 2. They include goal-oriented criteria such as "Understanding the Science" and "Understanding the Processes of Inquiry," process-oriented criteria such as "Being Systematic" and "Reasoning Carefully," and socially-oriented criteria such as "Communicating Well" and "Teamwork." These characterizations of good work are used not only by the teachers in judging the students' research projects, but also by the students themselves. At the beginning of the curriculum, the criteria are introduced and explained to the students as the "Guidelines for Judging Research" (see Figure 2). Then, at the end of each phase in the Inquiry Cycle, the students monitor their progress by evaluating their work on the two most relevant criteria. At the end of each module, they reflect on their work by evaluating themselves on all of the criteria. Similarly, when they present their research projects to the class, the students evaluate not only their own research projects but also each others. They give each other feedback both verbally and in writing. These assessment criteria are thus used as a way of helping to introduce students to the characteristics of good research, and to monitoring and reflecting on their inquiry processes. In what follows, we present sample excerpts from a class's reflective assessment discussion. Students give oral presentations of their projects accompanied by a poster, and they answer questions about their research. Following each presentation, the teacher picks a few of the assessment criteria and asks students in the audience how they would rate the students' presentation. In these conversations, students are typically respectful of one another and generally give their peers high ratings (i.e., ratings of 3-5 on a 5-point scale). However, within the range of high scores that they use, they do make distinctions among the criteria and offer insightful evaluations of the projects that have been presented. The following presents some examples of such reflective assessment conversations. (Pseudonyms are used throughout, and the transcript has been lightly edited to improve its readability.) Teacher: Ok, now what we are going to do is give them some feedback. What about their "understanding the process of inquiry"? In terms of their following the steps within the Inquiry Cycle, on a scale from 1 to 5, how would you score them? Vanessa. Vanessa: I think I would give them a 5 because they followed everything. First they figured out what they wanted to inquire, and then they made hypotheses, and then they figured out what kind of experiment to do, and then they tried the experiment, and then they figured out what the answer really was and that Jamal's hypothesis was correct. Teacher: All right, in terms of their performance, "being inventive." Justin? Justin: Being inventive. I gave them a 5 because they had completely different experiments than almost everyone else's I've seen. So, being inventive, they definitely were very inventive in their experimentation. Teacher: Ok, good. What about "reasoning carefully?" Jamal, how would you evaluate yourself on that? Jamal: I gave myself a 5, because I had to compute the dotprints between the experiments we did on mass. So, I had to compute everything. And, I double checked all of my work. Teacher: Great. Ok, in terms of the social context of work, "writing and communicating well." Carla, how did you score yourself in that area? Carla: I gave myself a 4, because I always told Jamal what I thought was good or what I thought was bad, and if we should keep this part of our experiment or not. We would debate on it and finally come up with an answer. Teacher: What about "teamwork?" Does anyone want to rate that? Teamwork. Nisha. Nisha: I don't know if I can say because I didn't see them work. (laughter) Teacher: That's fine. That's fair. You are being honest. Julia? Julia: I gave them a 5 because they both talked in the presentation, and they worked together very well, and they looked out for each other. There are various arguments for why incorporating such a Reflective-Assessment Process into the curriculum should be effective. One is the "transparent assessment" argument put forward by Frederiksen and Collins (1989; Frederiksen, 1994), who argue that introducing students to the criteria by which their work will be evaluated enables students to better understand the characteristics of good performance. In addition, there is the argument about the importance of metacognition put forward by researchers (e.g., Baird, Fensham, Gunstone, & White, 1991; Brown 1984; Brown & Campione, 1996; Collins, Brown, & Newman, 1989; Miller, 1991; Reeve & Brown, 1985; Scardamalia, & Bereiter, 1991; Schoenfeld, 1987; Schon, 1987; Towler & Broadfoot, 1992) who maintain that monitoring and reflecting on the process and products of one's own learning is crucial to successful learning as well as to "learning how to learn." Research on good versus poor learners shows that many students, particularly lower-achieving students, have inadequate metacognitive processes and their learning suffers accordingly (Campione, 1984; Chi et. el., 1989). Thus if you introduce and support such processes in the curriculum, the students' learning and inquiry should be enhanced. Instructional trials of the ThinkerTools Inquiry Curriculum in urban classrooms (which included many lower-achieving students) provided an ideal opportunity to test these hypotheses concerning the utility of such a Reflective-Assessment Process.
Instructional Trials	INSTRUCTIONAL TRIALS OF THE THINKERTOOLS INQUIRY CURRICULUM In 1994, we conducted instructional trials of the ThinkerTools Inquiry Curriculum. Three teachers used it in their twelve urban classes in grades 7-9. The average amount of time they spent on the curriculum was 10.5 weeks. Two of the teachers had no prior formal physics education. They were all teaching in urban situations in which their class sizes averaged almost thirty students, two thirds of whom were minority students, and many were from highly disadvantaged backgrounds. We analyzed the effects of the curriculum for students who varied in their degree of educational advantage, as measured by their standardized achievement test scores (CTBS -- Comprehensive Test of Basic Skills). We compared the performance of these middle-schools students with that of high-school physics students. We also carried out a controlled study comparing ThinkerTools classes in which students engaged in the Reflective-Assessment Process with matched "Control" Classes in which they did not. For each of the teachers, half of his or her classes were Reflective-Assessment Classes and the other half were Control Classes. In the Reflective-Assessment Classes, the students were given the assessment framework (Figure 2) and they continually engaged in monitoring and evaluating their own and each other's research. In the Control Classes, the students were not given an explicit framework for reflecting on their research; instead, they engaged in alternative activities in which they commented on what they did and did not like about the curriculum. In all other respects, the classes participated in the same ThinkerTools inquiry-based science curriculum. There were no significant differences in students' average CTBS scores for the classes that were randomly assigned to the different treatments (reflective-assessment vs. control), for the classes of the three different teachers, or for the different grade levels (7th, 8th, and 9th). Thus, the classes were all comparable with regard to achievement test scores.
Results	AN OVERVIEW OF THE RESULTS Our results show that the curriculum and software modeling tools make the difficult subject of physics understandable and interesting to a wide range of students. Further, the focus on creating models enables students to learn not only about physics, but also about the properties of scientific models and the inquiry processes needed to create them. In addition, engaging in inquiry also improves students' attitudes toward learning and doing science (White & Frederiksen, 1998).
	The Development of Inquiry Expertise One of our assessments of students' scientific inquiry expertise was an inquiry test that was given both before and after the ThinkerTools Inquiry Curriculum. In this written test, the students were asked to investigate a specific research question: "What is the relationship between the weight of an object and the effect that sliding friction has on its motion?" In this test, the students were asked to come up with alternative, competing hypotheses with regard to this question. Next, they had to design on paper an experiment that would determine what actually happens, and then they had to pretend to carry out their experiment. In other words, they had to conduct it as a thought experiment and make up the data that they thought they would get if they actually carried out their experiment. Finally, they had to analyze their made-up data to reach a conclusion and relate this conclusion back to their original, competing hypotheses. In scoring this test, the focus was entirely on the students' inquiry process. Whether or not the students' theories embodied the correct physics was regarded as totally irrelevant. Figure 5 presents the gain scores on this test for both low and high achieving students, and for students in the Reflective Assessment and Control Classes. Notice, firstly, that students in the Reflective Assessment Classes gained more on this inquiry test. Secondly, notice that this was particularly true for the low-achieving students. This is the first piece of evidence that the metacognitive, Reflective Assessment Process is beneficial, particularly for academically disadvantaged students.

	Figure 5. The mean gain scores on the Inquiry Test for students in the Reflective Assessment and Control Classes, plotted as a function of their achievement level.
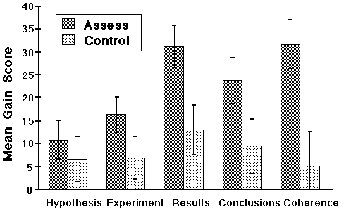
	If we examine this finding in more detail by looking at the gain scores for each component of the inquiry test, as shown in Figure 6, one can see that the effect of Reflective Assessment is greatest for the more difficult aspects of the test: making up results, analyzing those made-up results, and relating them back to the original hypotheses. In fact, the largest difference in the gain scores is that for a measure we call "coherence," which measures the extent to which the experiments that the students designed address their hypotheses, their made-up results relate to their experiments, their conclusions follow from their results, and whether they relate their conclusions back to their original hypotheses. This kind of overall coherence in research is, we think, a very important indication of sophistication in inquiry. It is on this coherence measure that we see the greatest difference in favor of students who engaged in the metacognitive Reflective-Assessment Process.

	Figure 6. Mean gains on the Inquiry Test Subscores for students in the Reflective Assessment and Control Classes.
	Next, we turn to presenting the results from the students' research projects. Students carried out two research projects, one about half way through the curriculum and one at the end. For the sake of brevity, we added the scores for these two projects together as shown in Figure 7. These results indicate that students in the Reflective Assessment Classes do significantly better on their research projects than students in the Control Classes. The results also show that the Reflective Assessment Process is particularly beneficial for the low-achieving students: low-achieving students in the Reflective Assessment Classes perform almost as well as the high-achieving students. These findings were the same across all three teachers and all three grade levels.

	Figure 7. The mean overall scores on their research projects for students in the Reflective Assessment and Control Classes, plotted as a function of their achievement level.
	The Development of Physics Expertise We now summarize the results from the point of view of the students' understanding of physics. We gave the students a general force-and-motion physics test, both before and after the ThinkerTools curriculum, that includes items in which students are asked to predict and explain how forces will affect an objects' motion (such as that shown in Figure 8). On this test we found significant pre-test to post-test gains. We also found that our middle-school, ThinkerTools students do better on such items than do high-school physics students who are taught using traditional approaches. Furthermore, when we analyzed the effects of the curriculum on items that represent near or far transfer in relation to contexts they had studied in the course, we found that there were significant learning effects for both the near and far transfer items. Together, these results show that you can teach sophisticated physics in urban, middle-school classrooms when you make use of simulation tools combined with scaffolding the inquiry process. In general, this inquiry-oriented, constructivist approach appears to make physics interesting and accessible to a wider range of students than is possible with traditional approaches (White, 1993a, White & Frederiksen, 1998; White & Horwitz, 1988).
	Circle the path the ball would take as it falls to the ground.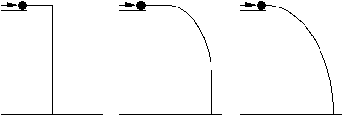 Explain the reasons for your choice:
	Figure 8. A sample problem from the physics test. On a set of such items, the ThinkerTools students averaged 68% correct and significantly outperformed the high-school physics students who averaged 50% correct (t343 = 4.59, p =<.001).
	What is the effect of the Reflective Assessment Process on the learning of physics? The assessment criteria were chosen to address principally the process of inquiry and only indirectly the conceptual model of force and motion that students are attempting to construct in their research. Moreover, within the curriculum students practice Reflective Assessment primarily in the context of judging their own and others' work on projects, not their progress in solving physics problems. Nonetheless, our hypothesis is that the Reflective Assessment should have an influence on students' success in developing conceptual models for the physical phenomena they have studied, through its effect in improving the learning of inquiry skills that are instrumental in their developing an understanding of physics principles. To evaluate the effects of Reflective Assessment on students' conceptual model for force and motion, we developed a Conceptual Model Test. Our findings, presented in Figure 9, show that the effects of Reflective Assessment extend to students' learning the science content as well as to their learning the processes of scientific inquiry, and that the benefits of Reflective Assessment are again greatest for the academically disadvantaged students.

	Figure 9. The mean scores on the Conceptual Model Test for students in the Reflective Assessment and Control Classes, plotted as a function of their achievement level.
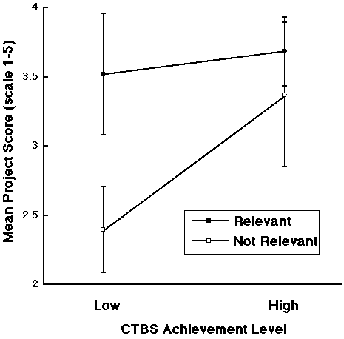
	The Impact of Understanding the Reflective Assessment Criteria If we are to attribute these effects of introducing Reflective Assessment to students' developing metacognitive competence, we need to show that the students developed an understanding of the assessment criteria and could use them to describe multiple aspects of their work. One way to evaluate their understanding of the assessment concepts is to compare their use of the criteria in rating their own work with the teachers' evaluation of their work using the same criteria. If students have learned how to use the criteria, their self-assessment ratings should correlate with the teachers' ratings for each of the criteria. We found that students in the Reflective-Assessment Classes, who worked with the criteria throughout the curriculum, showed significant agreement with the teachers in judging their work, while this was not the case for students in the Control Classes, who were given the criteria only at the end of the curriculum for judging their final projects. For example, in judging Reasoning Carefully, students who worked with the assessment criteria throughout the curriculum had a correlation of .58 between their ratings of Reasoning Carefully on their final projects and the teachers'. The average correlation for these students over all of the criteria was .48, which is twice that for students in the Control Classes. If the Reflective-Assessment Criteria are acting as metacognitive tools to help students as they ponder the functions and outcomes of their inquiry processes, then the students' performance in developing their inquiry projects should depend upon how well they have understood the assessment concepts. To evaluate their understanding, we rated whether the evidence they cited in justifying their self assessments was or was not relevant to the particular criterion they were considering. We then looked at the quality of the students' final projects, comparing students who had developed an understanding of the set of assessment concepts by the end of the curriculum with those who did not. Our results, shown in Figure 10, indicate that students who had learned to use the interpretive concepts appropriately in judging their work produced higher quality projects than students who had not. And again we found that the benefit of learning to use the assessment criteria was greatest for the low-achieving students.

	Figure 10. The mean scores on their Final Projects for students who did and did not provide relevant evidence when justifying their self-assessment scores, plotted as a function of their achievement level.
	Taken together, these research findings clearly implicate the use of the assessment criteria as a reflective tool for learning to carry out inquiry. Students in the Reflective-Assessment Classes generated higher scoring research reports than those in the Control Classes. Further, students who showed a clear understanding of the criteria produced higher quality investigations than those who showed less understanding. Thus, there are strong beneficial effects of introducing a metacognitive language to facilitate students' reflective explorations of their work in classroom conversations and in self assessment An important finding was that the beneficial effect of Reflective Assessment was particularly strong for the lower-achieving students: The Reflective-Assessment Process enabled the lower-achieving students to gain more on the inquiry test (see Figure 5). It also enabled them to perform close to the higher-achieving students on their research projects (see Figure 7). The introduction of Reflective Assessment, while helpful to all, was thus closing the performance gap between the lower and higher-achieving students. In fact, the Reflective-Assessment Process enabled lower-achieving students to perform equivalently to higher-achieving students on their research projects when they did their research in collaboration with a higher-achieving student. In the Control Classes, in contrast, the lower-achieving students did not do as well as high-achieving students, regardless of whether or not they collaborated with a higher-achieving student. Thus, there was evidence that social interactions in the Reflective-Assessment Classes--particularly those between lower and higher-achieving students--were important in facilitating learning (cf., Carter & Jones, 1994; Slavin, 1995; and Vygotsky, 1978).
Findings	THE IMPLICATIONS OF OUR FINDINGS We think that our findings have strong implications for what such inquiry-oriented, metacognitively-focused curricula can accomplish in an urban school setting. In particular, we argue that three important conclusions follow from our work: To be equitable, science curricula should incorporate reflective inquiry, and assessments of students' learning should include measures of inquiry expertise. Students should learn how to transfer the inquiry and reflective assessment processes to other domains so that they "learn how to learn" and can utilize these valuable metacognitive skills in their learning of other school subjects. Such an inquiry-oriented approach to education, in which the development of metacognitive knowledge and skills plays a central role, should be introduced early in the school curriculum (i.e., at the elementary school level). 1. Science curricula should incorporate inquiry and include assessments of students' inquiry expertise. Our results suggest that, from an equity standpoint, curricular approaches can be created that are not merely equal in their value for, but actually enhance the learning of less-advantaged students. Furthermore, to adequately and fairly assess the effectiveness of such curricula, one needs to utilize measures of inquiry expertise, such as our inquiry tests and research projects. If only subject-matter tests are used, the results can be biased against both low-achieving students and female students. For instance, on the research projects, we found that low-achieving students who had the benefit of the Reflective-Assessment Process did almost as well as the high-achieving students. And, these results could not be attributed simply to ceiling effects. We also found that the male and female students did equally well on the inquiry tests and research projects. On the physics tests, however, the pattern of results was not comparable: males outperformed females (on both pretests and posttests) and the high-achieving students outperformed the low-achieving students (White & Frederiksen, 1998). Thus utilizing inquiry tests and research projects in addition to subject-matter tests not only played a valuable role in facilitating the development of inquiry skills, it also produced a more comprehensive and equitable assessment of students' accomplishments in learning science. 2. It is desirable to help students transfer what they learn about inquiry and reflection to the rest of their school curriculum. Students' work in the ThinkerTools Inquiry Curriculum and their performance on the various inquiry assessments indicate that they acquired an understanding of the Inquiry Cycle as well as the knowledge needed to carry out each of the steps in this cycle. They also learned about the forms that scientific laws, models, and theories can take and of how the development of scientific theories is related to empirical evidence. In addition, they acquired the metacognitive skills of monitoring and reflecting on their inquiry processes. Since all of science can be viewed as a process of constructing models and theories, both the Inquiry Cycle and the Reflective Assessment Process can be applied to learning and doing all areas of science, not just physics. Thus understanding and engaging in the Inquiry Cycle and Reflective Assessment Process should benefit students in their future science courses. We see evidence of these benefits and transfer in the subsequent work of ThinkerTools students. For example, 8th grade students, who did ThinkerTools in the 7th grade, were asked to do research projects that used the Inquiry Cycle. They were free to choose topics other than physics; for instance, one group of students wanted to understand how listening to music affects one's performance on schoolwork. They did an experiment in which their classmates listened to different kinds of music while taking an arithmetic test. They wrote research reports that described how they followed the Inquiry Cycle in planning and carrying out their research, and they evaluated their own and each other's research using scoring criteria shown in Figure 2. Their teacher reports that their performance on these projects was equal to or better than the performance on their ThinkerTools physics projects. Further, at the end of the curriculum, some students were interviewed and asked if the Inquiry Cycle and Reflective Assessment Process could be used to help them learn other subjects. Many of their answers involved highly creative explanations of how it could be applied to domains such as history, mathematics, and English, as well as to other areas of science. With regard to the teachers, all of them attest to the benefits of both the Inquiry Cycle and the Reflective Assessment Process and have chosen to incorporate them into the other science courses that they teach. In order to make the valuable skills of inquiry, modeling, and reflection apply to other experimental sciences, such as biology, as well as to the learning of nonscience subjects, various approaches could be pursued. For instance, students could be introduced to a generalized version of the Inquiry Cycle (such as: Question, Hypothesize, Investigate, Analyze, Model, and Evaluate, which represents a minor transformation of the more experimentally-oriented Inquiry Cycle that students internalize during the ThinkerTools Inquiry Curriculum). This generalization could give students a metacognitive view of learning and inquiry that can be applied to any topic in which building predictive/explanatory models can become the focus. In addition, the students could discuss how the Reflective Assessment Process, which uses the criteria shown in Figure 2 (such as Making Connections, Reasoning Carefully, and Communicating Well), can readily be generalized to learning other science topics as well as to learning in general. Having such explicit discussions of transfer in conjunction with explicitly using versions of the Inquiry Cycle and Reflective Assessment Process in their science and other curricula should enable students and teachers to appreciate and benefit from the power of metacognition. Investigating how such generalization and transfer can be achieved will be a major focus of our future research (e.g., White, Shimoda, & Frederiksen, in press). 3. It is important to introduce inquiry-based learning and metacognition early in the school curriculum. Another major implication of our research is that inquiry and reflective assessment should be taught early. This would enable young students to develop metacognitive skills that are important components of expertise in learning. These skills should help the low-achieving students to overcome their educational disadvantages. Our results suggest that inquiry-based science could and should be introduced in the early grades. Students over a range of grades showed equal degrees of learning using the inquiry curriculum: We found no age differences in students' pretest or posttest scores on the inquiry test over grades ranging from grade 7 to grade 9, nor did we find any age differences in students' gains on the physics tests. In addition, our pretests showed only small gender differences in science content knowledge in the 7th grade, but these gender differences were much larger in the later grades (White, 1993a; White & Frederiksen, 1998). Together, these results suggest that inquiry-based science could be introduced in earlier grades (see also Metz, 1995), and that doing so in these grades (before gender differences in science content knowledge have developed) might help to eliminate the gender differences that develop in knowledge of and interest in science. We plan to extend our work on the ThinkerTools Inquiry Project to investigate how inquiry, modeling, and metacognition can be taught and assessed in earlier grades. To facilitate this investigation, were are developing a constructivist curriculum, similar to the existing ThinkerTools Inquiry Curriculum, in which low-achieving students work in partnership with high-achieving students to plan, carry out, and critically evaluate research. The subject matter is again the physics of force and motion which we conjecture is appropriate for elementary school students, who are often involved in sports and focused on the physical world in general. We further propose to help students learn to transfer the inquiry and metacognitive skills which they acquire in this domain to their other school subjects (as outlined above). Our hope is that such an inquiry-oriented curriculum which focuses on the development of metacognitive skills will enable all students to "learn how to learn" at an early age and will thereby help underprivileged students to overcome their educational disadvantages.
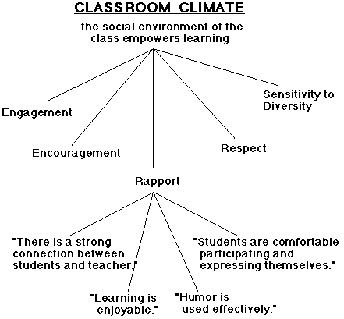
Teachers	METACOGNITIVE FACILITATION FOR TEACHERS We conclude by addressing the question: How can we enable teachers to implement such inquiry-oriented approaches to education? Our research in which we studied the dissemination of the ThinkerTools Inquiry Curriculum indicates that it is not sufficient to simply provide teachers with teacher's guides that attempt to outline goals, describe activities, and suggest, in a semi-procedural fashion, how the lessons might proceed (White & Frederiksen, 1998). We have found that teachers also need to develop a conceptual framework for characterizing good inquiry teaching and for reflecting on their teaching practices in the same way that students need to develop criteria for characterizing good scientific research and for reflecting on their inquiry processes. To achieve this goal, we utilized a framework that we developed for the National Board for Professional Teaching Standards (Frederiksen, Sipusic, Sherin, & Wolfe, 1997). This framework, which attempts to characterize expert teaching, includes five major criterion: worthwhile engagement, adept classroom management, effective pedagogy, good classroom climate, and explicit thinking about the subject matter, to which we added active inquiry. In this characterization of expert teaching, each of these criterion for good teaching is unpacked into a set of "aspects." For example, Figure 11 illustrates the criterion of "classroom climate," which is defined as "the social environment of the class empowers learning." Under this general criterion, there are five different aspects: engagement, encouragement, rapport, respect, and sensitivity to diversity. Each of these aspects is defined in terms of specific characteristics of classroom practice, such as "humor is used effectively" or "there is a strong connection between students and teacher." Further, each of these specific characteristics of classroom practice is indexed to video clips, called "video snippets," which illustrate it. This framework characterizes good inquiry teaching and provides teachers with video exemplars of teaching practice.

	Figure 11. An example of the hierarchical definitions created for each criterion, such as classroom climate, which are used to characterize expert teaching.
	Such materials can be used to enable teachers to learn about inquiry teaching and its value, as well as to reflect on their own and each others' teaching practices. For example, recently we tried the following approach with a group of ten student teachers. The student teachers first learned to use the framework outlined above by scoring videotapes of ThinkerTools classrooms. Then, they used the framework to facilitate discussions of videotapes of their own teaching. In this way, they participated in what we call "video clubs," which enabled them to reflect on their own teaching practices and to hopefully develop better approaches for inquiry teaching. (Video clubs incorporate social activities designed to help teachers reflectively assess and talk about their teaching practices [Frederiksen et al., 1997]). The results have been very encouraging, and our findings indicate that engaging in this reflective activity enabled the student teachers to develop a shared language for viewing and talking about teaching which, in turn, led to highly productive conversations in which they explored and reflected on their own teaching practices (Diston, 1997; Frederiksen & White, 1997; Richards & Colety, 1997). We conclude by arguing that the same emphases on metacognitive facilitation that we illustrated is important and effective for students is beneficial for teachers as well. It can enable teachers to explore the cognitive and social goals related to inquiry teaching and to thereby improve their own teaching practices. Through this approach, both students and teachers can come to understand the goals and processes related to inquiry, and can learn how to engage in effective inquiry learning and teaching.
Acknowledgments	ACKNOWLEDGMENTS We gratefully acknowledge the support our sponsors: the James S. McDonnell Foundation, the National Science Foundation, and the Educational Testing Service. The ThinkerTools Inquiry Project is a collaborative endeavor between researchers at UC Berkeley and ETS with middle-school teachers in the Berkeley and Oakland public schools. We would like to thank all members of the team for their valuable contributions to this work.
References	REFERENCES Baird, J., Fensham, P., Gunstone, R., & White, R. (1991). The importance of reflection in improving science teaching and learning. Journal of Research in Science Teaching, 28(2), 163-182. Brown, A. (1984). Metacognition, executive control, self-regulation, and other more mysterious mechanisms. In F. Weinert & R. Kluwe (Eds.), Metacognition, Motivation, and Learning, (pp. 60-108). Germany: Kuhlhammer. Brown, A., & Campione, J. (1996). Psychological theory and the design of innovative learning environments: On procedures, principles, and systems. In L. Schauble & R. Glaser (Eds.), Innovations in Learning: New Environments for Education, (pp. 289-325). Mahwah, NJ: Erlbaum. Brown, J., Collins, A., & Duguid, P. (1989). Situated cognition and the culture of learning. Educational Researcher, 18, 32-42. Bruer, J. (1993). Schools for Thought: A Science of Learning in the Classroom. Cambridge, MA: MIT Press. Campione, J. (1984). Metacognitive components of instructional research with problem learners. In F. Weinert & R. Kluwe (Eds.), Metacognition, Motivation, and Learning, (pp. 109-132). West Germany: Kuhlhammer. Carter, G., & Jones, M. (1994). Relationship between ability-paired interactions and the development of fifth graders' concepts of balance. Journal of Research in Science Teaching, 31, 8, 847-856. Chi, M., Bassock, M., Lewis, M., Reimann, P., & Glaser, R. (1989). Self-explanations: How students study and use examples in learning to solve problems. Cognitive Science, 13, 145-182. Collins, A., Brown J., & Newman, S. (1989). Cognitive apprenticeship: Teaching the craft of reading, writing, and mathematics. In L, Resnick (Ed.), Knowing, Learning, and Instruction: Essays in Honor of Robert Glaser, (pp. 453-494). Mahwah, NJ: Erlbaum. Collins, A., and Ferguson, W. (1993). Epistemic forms and epistemic games: Structures and strategies to guide inquiry. Educational Psychologist, 28, 25-42. Diston, J. (1997). Seeing teaching in video: Using an interpretative video framework to broaden pre-service teacher development. Unpublished master's project, Graduate School of Education, University of California, Berkeley, CA. Frederiksen, J. (1994). Assessment as an agent of educational reform. The Educator, 8(2), 2-7. Frederiksen, J., & Collins, A. (1989). A systems approach to educational testing. Educational Researcher, 18(9), 27-32. Frederiksen, J., Sipusic, M., Sherin, M., & Wolfe, E. (1997). Video portfolio assessment: Creating a framework for viewing the functions of teaching (Technical Report of the Cognitive Science Research Group). Oakland, CA: Educational Testing Service. Frederiksen, J. R., & White, B. Y. (1997). Cognitive facilitation: A method for promoting reflective collaboration. In Proceedings of the Second International Conference on Computer Support for Collaborative Learning. Mahwah, NJ: Erlbaum. Hatano, G., & Inagaki, K. (1991). Sharing cognition through collective comprehension activity. In L. Resnick, J. Levine, S. Teasley (Eds.), Perspectives on Socially Shared Cognition (pp. 331-348). Washington, DC: American Psychological Association. Metz, K. (1995). Reassessment of developmental constraints on children's science instruction. Educational Researcher, 65(2), 93-127. Miller, M. (1991). Self-assessment as a specific strategy for teaching the gifted learning disabled. Journal for the Education of the Gifted, 14(2), 178-188. Nickerson, R., Perkins, D., & Smith, E. (1985). The Teaching of Thinking. Mahwah, NJ: Erlbaum. Palincsar, A. & Brown, A. (1984). Reciprocal teaching of comprehension fostering and monitoring activities. Cognition and Instruction, 1(2), 117-175. Reeve, R. A., & Brown, A. L. (1985). Metacognition reconsidered: implications for intervention research. Journal of Abnormal Child Psychology, 13(3), 343-356. Resnick, L. (1987). Education and Learning to Think. Washington, D. C.: National Academy Press. Richards, S., & Colety, B. (1997). Conversational analysis of the MACSME video analysis class: Impact on and recommendations for the MACSME program. Unpublished master's project, Graduate School of Education, University of California, Berkeley, CA. Scardamalia, M., & Bereiter, C. (1991). Higher levels of agency for children in knowledge building: A Challenge for the Design of New Knowledge Media. The Journal of the Learning Sciences, 1(1), 37-68. Schoenfeld, A. H. (1987). What's all the fuss about metacognition? In A. H. Schoenfeld (Ed.), Cognitive Science and Mathematics Education (pp. 189-215). Mahwah, NJ: Erlbaum. Schon, D. (1987). Educating the Reflective Practitioner. San Francisco, CA: Josey-Bass Publishers. Slavin, R. (1995). Cooperative learning: theory, research, and practice (2nd edition). Needham Heights, MA: Allyn and Bacon. Towler, L., & Broadfoot, P. (1992). Self-assessment in primary school. Educational Review, 44(2), 137-151. Vygotsky, L. (1978). Mind in Society: The Development of Higher Psychological Processes. (M. Cole, V. John-Steiner, S. Scribner, & E. Souberman, Eds. and Trans.). Cambridge, England: Cambridge University Press. White, B. (1993a). ThinkerTools: Causal models, conceptual change, and science education. Cognition and Instruction, 10(1), 1-100. White, B. (1993b). Intermediate causal models: A missing link for successful science education? In R. Glaser (Ed.), Advances in Instructional Psychology, Volume 4, (pp. 177-252). Mahwah, NJ: Erlbaum. White, B., & Frederiksen, J. (1998). Inquiry, modeling, and metacognition: Making science accessible to all students. Cognition and Instruction, 16(1), 3-117. White, B., & Horwitz, P. (1988). Computer microworlds and conceptual change: A new approach to science education. In P. Ramsden (Ed.), Improving learning: New perspectives. London: Kogan Page. White, B., Shimoda, T., & Frederiksen, J. (in press). Constructing a theory of mind and society: ThinkerTools that support students' metacognitive and metasocial development. In S. Lajoie (Ed.), Computers as Cognitive Tools: The Next Generation. Mahwah, NJ: Erlbaum.
Appendix	APPENDIX A This appendix contains the following: The outline for research reports that is given to students. An example of a student's research report and her self-assessment.
	An Outline and Checklist for Your Research Reports Question: Clearly state the research question. Predict: What hypotheses did you have about possible answers to the question? Explain the reasoning behind each of your hypotheses. Experiment: Describe your computer experiment(s). Draw a sketch of your computer model. Describe how you used it to carry out your experiment(s). Show your data in tables, graphs, or some other representation. Describe your real-world experiment(s). Draw a sketch of how you set up the lab equipment. Describe how you used the equipment to carry out your experiment(s). Show your data in tables, graphs, or some other representation. Model: Describe how you analyzed your data and show your work. Summarize your conclusions. Which of your hypotheses does your data support? State any laws that you discovered. What is your theory about why this happens? Apply: Show how what you learned could be useful. Give some examples. What are the limitations of your investigation? What remains to be learned about the relationship between the mass of an object and how forces affect its motion? What further investigations would you do if you had more time?
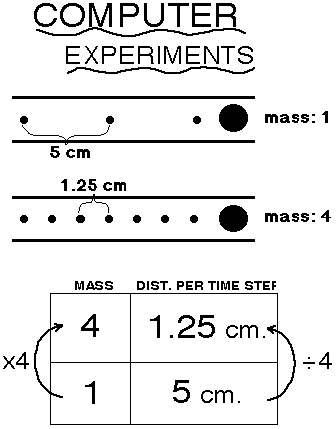
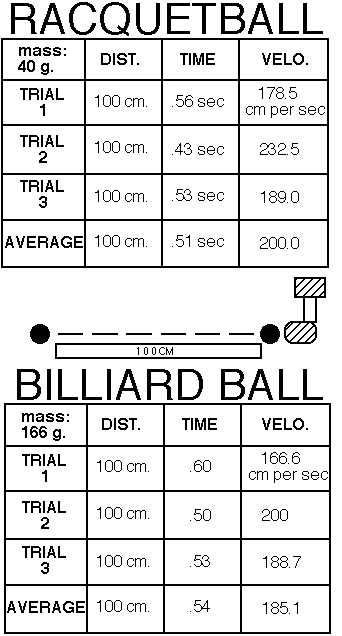
	An example research report about mass and motion written by a 7th grade student (age 12) During the past few weeks, my partner and I have been creating and doing experiments and making observations about mass and motion. We had a specific question that we wanted to answer -- how does the mass of a ball affect its speed? I made some predictions about what would happen in our experiments. I thought that if we had two balls of different masses, the ball with the larger mass would travel faster, because it has more weight to roll forward with, which would help push it. We did two types of experiments to help us answer our research question -- computer and real world. For the computer experiment, we had a ball with a mass of 4 and a ball with a mass of 1. In the real world they are pretty much equal to a billiard ball and a racquetball. We gave each of the balls 5 impulses, and let them go. Each of the balls left dotprints, that showed how far they went for each time step. The ball with the mass of 4 went at a rate of 1.25 cm per time step. The ball with the mass of 1 went at a rate of 5 cm per time step, which was much faster. For the real world experiment, we took a billiard ball (with a mass of 166 gms) and a racquetball (with a mass of 40 gms). We bonked them once with a rubber mallet on a linoleum floor, and timed how long it took them to go 100 cm. We repeated each experiment 3 times and then averaged out the results, so our data could be more accurate. The results of the two balls were similar. The racquetball's average velocity was 200 cm per second, and the billiard ball's was 185.1 cm per second. That is not a very significant difference, because the billiard ball is about 4.25 times more massive than the racquetball. We analyzed our data carefully. We compared the velocities, etc. of the lighter and heavier balls. For the computer experiment, we saw that the distance per time step increased by 4 (from 1.25 cm to 5 cm) when the mass of the ball decreased by 4 (from 4 to 1). This shows a direct relationship between mass and speed. It was very hard to analyze the data from our real world experiment. One reason is that it varies a lot for each trial that we did, so it is hard to know if the conclusions we make will be accurate. We did discover that the racquetball, which was lighter, traveled faster than the billiard ball, which was heavier. Our data doesn't support my hypothesis about mass and speed. I thought that the heavier ball would travel faster, but the lighter one always did. I did make some conclusions. From the real world experiment I concluded that the surface of a ball plays a role in how fast it travels. This is one of the reasons that the two balls had similar velocities in our real world experiment. (The other reason was being inaccurate). The racquetball's surface is rubbery and made to respond to a bonk and the billiard ball's surface is slippery and often makes it roll to one side. This made the balls travel under different circumstances, which had an effect on our results. From the computer experiment I concluded that a ball with a smaller mass goes as many times faster than a ball with a larger mass as it is lighter than it. This happens because there is a direct relationship between mass and speed. For example, if you increase the mass of a ball then the speed it travels at will decrease. I concluded in general, of course, that if you have two balls with different masses that the lighter one will go faster when bonked, pushed, etc. This is because the ball doesn't have as much mass holding it down. The conclusions from our experiments could be useful in real world experiences. If you were playing baseball and you got to choose what ball to use, you would probably choose one with a rubbery surface that can be gripped, over a slippery, plastic ball. You know that the type of surface that a ball has effects how it responds to a hit. If you were trying to play catch with someone you would want to use a tennis ball rather than a billiard ball, because you know that balls with smaller masses travel faster and farther. The investigations that we did do have limitations. In the real world experiments the bonks that we gave the balls could have been different sizes, depending on who bonked the ball. This would affect our results and our conclusions. The experiment didn't show us how fast balls of different masses and similar surfaces travel in the real world. That is something we still can learn about. If there was more time, I would take two balls of different masses with the same kind of surface and figure out their velocities after going 100 cm. Overall, our experiments were worthwhile. They proved an important point about how mass affects the velocity of a ball. I liked being able to come up with my own experiments and carrying them out.



	An example of a self assessment written by the student who wrote the preceding research report (age 12) UNDERSTANDING

	Justify your score based on your work. I have a basically clear understanding of how mass affects the motion of a ball in general, but I don't have a completely clear sense of what would happen if friction, etc. was taken into account.

	Justify your score based on your work. I used the inquiry cycle a lot in my write up, but not as much while I was carrying out my experiments.

	Justify your score based on your work. I made some references to the real world, but I haven't fully made the connection to everyday life.
	PERFORMANCE: DOING SCIENCE

	Justify your score based on your work. What I did was original, but many other people were original and did the same (or similar) experiment as us.

	Justify your score based on your work. On the whole I was organized, but if I had been more precise my results would have been a little more accurate.

	Justify your score based on your work. I used many of the tools I had to choose from. I used them in the correct way to get results.

	Justify your score based on your work. I took into account the surfaces of the balls in my results, but I didn't always reason carefully. I had to ask for help, but I did compute out our results mathematically.
	SOCIAL CONTEXT OF WORK

	Justify your score based on your work. I understand the science, but in my writing and comments I might have been unclear to others.

	Justify your score based on your work. We got along fairly well and had a good project as a result. However, we had a few arguments.
	REFLECTION

	How well do you think you evaluated your work using this scorecard? I think I judged myself fairly - not too high or too low. I didn't always refer back to specific parts of my work to justify my score.
	copyright 2000 ThinkerTools project